Nesse artigo será abordado operações com matrizes, tipos de matrizes e alguns exercicios de vestibulares passados para fixação da matéria e preparação para o vestibular.
Matrizes
As matrizes são estruturas matemáticas organizadas na forma de tabela com linhas e colunas, utilizadas na organização de dados e informações e dispostos em m linhas e n colunas.
.jpg) ,
, matriz de ordem 3 x 1. (3 linhas e 1 coluna).
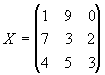 ,
, matriz de ordem 3 x 3. (3 linhas e 3 colunas).
.jpg) ,
, matriz de ordem 4 x 2. (4 linhas e 2 colunas)
Transposta de uma matriz A : é a matriz At obtida de A permutando-se as linhas pelas colunas e vice-versa.
Exemplo:
A matriz At é a matriz transposta da matriz A .
Adição de matrizes
Esta operação só pode ser feita com matrizes de mesmo número de linhas e mesmo número de colunas (mesma ordem). A soma dessas matrizes irá resultar em outra matriz que também terá o mesmo número de linhas e de colunas.
Os termos deverão ser somados com os seus termos correspondentes.
Concluímos que:
Dada duas matrizes, A e B, as duas de ordem m x n. Então, A + B = C, com
C de ordem m x n ↔ a11 + b11 = c11.
Observe os exemplos seguintes para melhor compreensão.
Exemplo: Dadas as matrizes abaixo, efetue A + B.
Solução: Temos que:
Subtração de matrizes
Dadas duas matrizes de mesmo tipo
, A e B, denomina-se matriz diferença (A-B) a matriz obtida subtraindo-se os elementos correspondentes de A e B. As matrizes subtraídas devem ter a mesma ordem (mesmo número de linhas e colunas) e a matriz obtida com a subtração (matriz diferença) também deve ter o mesmo número de linhas e colunas que as matrizes subtraídas.
Concluímos que:
Dada duas matrizes, A e B, as duas de ordem m x n. Então A – B = C de
ordem m x n ↔ a11 – a11 = c11
Exemplo: Considerando as matrizes abaixo, efetue A – B.
Solução: Temos que:
Produto das matrizes
Dada uma matriz A = (aij)mxn e um número real k, denomina-se matriz produto do numero real K por A, a matriz obtida multiplicando-se cada um dos seus elementos por k.
Em outras palavras, cada elemento de C é calculado multiplicando-se ordenadamente os elementos da linha i da matriz A pelos elementos correspondentes da coluna j da matriz B e , a seguir, somando-se os produtos obtidos. Veja abaixo:
Vamos mostrar o produto de matrizes com um exemplo:
Onde L1C1 é o produto escalar dos elementos da linha 1 da 1ª matriz pelos elementos da coluna1 da segunda matriz, obtido da seguinte forma:
L1C1 = 3.2 + 1.7 = 13. Analogamente, teríamos para os outros elementos:
L1C2 = 3.0 + 1.5 = 5
L1C3 = 3.3 + 1.8 = 17
L2C1 = 2.2 + 0.7 = 4
L2C2 = 2.0 + 0.5 = 0
L2C3 = 2.3 + 0.8 = 6
L3C1 = 4.2 + 6.7 = 50
L3C2 = 4.0 + 6.5 = 30
L3C3 = 4.3 + 6.8 = 60, e, portanto, a matriz produto será igual a:
O produto entre duas matrizes A e B é definido se , e somente se, o número de colunas da matriz A for igual ao numero de linhas da matriz B. Assim:
MATRIZ QUADRADA
É A MATRIZ CUJO NÚMERO DE LINHAS É IGUAL AO DE COLUNAS. PORTANTO, SE AM×N É QUADRADA, M = N. EXEMPLO:

QUANDO A MATRIZ É QUADRADA NELA PODEMOS PERCEBER A PRESENÇA DE UMA DIAGONAL SECUNDÁRIA E UMA DIAGONAL PRINCIPAL.

MATRIZ IDENTIDADE
Para que seja uma matriz identidade uma matriz tem que ser quadrada do tipo: 2x2 , 3x3, 4x4, etc. e os elementos da diagonal principal devem ser iguais a 1 e os outros elementos iguais a 0.
Exemplo:
Matriz diagonal
Para que seja uma matriz diagonal uma matriz tem que ser quadrada do tipo: 2x2, 3x3, 4x4, etc. e os elementos que não são da digonal principal devem ser iguais a zero.
Matriz inversa
Considere uma matriz quadrada A de ordem n. Se existir uma matriz quadrada B, da mesma ordem, tal que: AB = In sendo In a matriz identidade, ou seja, uma matriz terá uma matriz inversa se for quadrada e se o produto das duas matrizes for igual a uma matriz identidade quadrada de mesma ordem das outras.
Então a matriz B será chamada inversa da matriz A, sendo indicada por A(-1). Nesse caso dizemos que a matriz é inversível. Se não existir a matriz B, dizemos que a matriz A não tem inversa, ou seja, não é inversível. Se a matriz inversa existir, ela é única.
Exemplo:
Determinar, se existir, a inversa da matriz A =  e B=
e B= 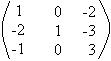 são inversas entre si.
são inversas entre si.
Para que seja verdade o produto de G . K = I3 Portanto, concluímos que as matrizes A e B são inversas entre si.
Portanto, concluímos que as matrizes A e B são inversas entre si.
Exercícios Matrizes
1) Multiplicando-se uma matriz 3 x 4 por uma matriz 4 x 5 obtém-se uma matriz de que tipo? a a2) (UNICAMP) Supondo a ≠ 0, determine x tal que A² = 0, onde A é a matriz A = (x x ).
3) Na matriz B = (bij)3x3, onde bij = -2, se i < j , calcule a12*a22*a32. 5i, se i = j 3ij, se i > j
4) Adicione as matrizes e determine os valores das incógnitas.
5) (MACK) Se A é uma matriz 3 x 4 e B uma matriz n x m, então:
a) existe A + B se, e somente se, n = 4 e m = 3;
b) existe AB se, e somente se, n = 4 e m = 3;
c) existem AB e BA se, e somente se, n = 4 e m = 3;
d) existem, iguais, A + B e B + A se, e somente se, A = B;
e) existem, iguais, AB e BA se, e somente se, A = B.
6) (PUC) Se A, B e C são matrizes quadradas e At, Bt e Ct são suas matrizes transpostas, e igualdade falsa entre essas matrizes é:
a) (A = B) . C = A . C + B . C
b) (A + B)t = At + Bt
c) (A . B)t = At . Bt
d) (A - B)C = AC - BC
e) (At)t = A
7) Caso exista, encontre a inversa da matriz  Gabarito: 1) 3 x 5 2) x = - a ou x = 0 3) - 360 4) x = 5 y = - 4 t = 1 z = 6 5) C 6) C 7)
Gabarito: 1) 3 x 5 2) x = - a ou x = 0 3) - 360 4) x = 5 y = - 4 t = 1 z = 6 5) C 6) C 7).jpg)

 ,
, , a qual, usando-se da tabela acima, será dado por:
, a qual, usando-se da tabela acima, será dado por: .
. , transmite-se a mensagem "PAZ" através da multiplicação das matrizes M e C, ou seja:
, transmite-se a mensagem "PAZ" através da multiplicação das matrizes M e C, ou seja: .
.


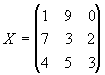 ,
, .jpg) ,
, 


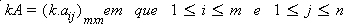

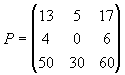
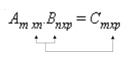





.jpg)