Salas montadas de 2015

O seminarista:um romance contra o celibato religioso

No interior de Minas Gerais, Eugênio, filho de fazendeiros, passa a infância ao lado de Margarida, filha de uma simples agregada da fazenda. Dessa convivência nasce o amor. Para evitar que o caso de amor progrida, os pais de Eugênio o internam em um seminário, obrigando-o a seguir a carreira eclesiática. O tempo passa mas Eugênio não esquece Margarida. Com a ajuda dos padres, seus pais inventam a notícia do casamento da moça, o que desilude Eugênio e o faz decidir-se pela vida de padre.

Certo dia,porém, ao voltar para a vila natal, ele é chamado a socorrer uma moça doente. Era Margarida. Ela lhe conta toda a verdade: tinha sido expulsa da fazenda, com a sua mãe, já morta, passava necessidades e não tinha casado com ninguém, pois ainda o amava. A paixão renasce com aquela visita e no dia seguinte os dois entregam-se ao amor.

Atormentado pelo remorso, Eugênio se prepara para rezar sua primeira missa quando alguém o chama para encomendar um cadáver que acabou de chegar à igreja. Era o corpo de Margarida. Eugênio não resiste ao choque e na hora da missa enlouquece.

Em O seminarista, Bernardo Guimarães faz um típico romance de tese, querendo provar o equívoco do celibato religioso, que deforma o homem, e do autoritarismo familiar, que não permite ao jovem seu próprio caminho na vida.

1. Você observou que nessa cena Eugênio e Mar

Para os alunos do terceiros anos

Queridos Formandos Parabens a vocês Pela sua conquista do terceiro anos, Aqueles que Repitirem de ano e porque você repetente Não esta Pronto para proxima fase da sua vida ja os que passaram parabens que aproveite esse momento especial e que eu dono desse blog eu vou tentar estar na formatura não prometo nada 

Matematica

(UFRJ) Uma confecção vai fabricar 3 tipos de roupas utilizando 3 materiais diferentes. Considere a matriz A abaixo, onde cada elemento a_ij representa quantas unidades de material j serão empregados para fabricação de roupas do tipo i.

a) Quantas unidades de material 3 serão empregados na confecção de uma roupa tipo 2?
b) Calcule o total de unidades do material 1 que será empregado para fabricar cinco roupas do tipo 1, quatro roupas do tipo 2 e duas roupas do tipo 3.

---

Solução: De acordo com o enunciado, temos a tabela:

	Material 1	Material 2	Material 3
Roupa tipo 1	5	0	2
Roupa tipo 2	0	1	3
Roupa tipo 3	4	2	1

a) O número de unidades de material j = 3 na confecção de uma roupa tipo i = 2 é o elemento a₂₃ da matriz A, ou melhor, é o elemento da segunda linha com a terceira coluna a₂₃ = 3 unidades.
b) O valor procurado é 5a₁₁ + 4a₂₁ + 2a₃₁ = 5×5 + 4×0 + 2×4 = 25 + 0 + 8 = 33 unidades.

---

---

Dada a matriz
,
calcule -a₁₂×a₂₁ + a₁₁×a₂₂ =

---

---

Solução: -a₁₂×a₂₁ + a₁₁×a₂₂ = = -(2)×1+2×(-1) = -2 - 2 = -4.
Nota: Este procedimento é usualmente chamado de cálculo do determinante da matriz A.

---

---

(PUC) Um batalhão do exército, resolveu codificar suas mensagens através da multiplicação de matrizes. Primeiramente, associa as letras do alfabeto aos números, segundo a correspondência abaixo considerada:

A	B	C	D	E	F	G	H	I	J	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25

Desta forma, supondo que o batalhão, em questão, deseja enviar a mensagem "PAZ", pode-se tomar uma matriz 2x2, da forma:
, a qual, usando-se da tabela acima, será dado por:
.
Tomando-se a matriz-chave C para o código, isto é:
, transmite-se a mensagem "PAZ" através da multiplicação das matrizes M e C, ou seja:
.
Ou através da cadeia de números 31 47 50 75. Desta forma, utilizando-se a mesma matriz-chave C, a decodificação da mensagem 51 81 9 14 será compreendida pelo batalhão como a transmissão da palavra:
(A) LUTE
(B) FOGO
(C) AMOR
(D) VIDA
(E) FUGA

---

Solução: Esta é uma das inúmeras aplicações das matrizes: escrever mensagens em códigos, de modo que somente pessoas autorizadas possam decifrá-las (Criptografia básica). Como a matriz C codifica a mensagem, para decodificar temos que multiplicar por uma matriz D que desfaz o que matriz C faz, ou seja, temos que multiplicar pela matriz D inversa de C. 
Para construir a Matriz D vamos usar o fato de que D é a matriz inversa de C se , e somente se, C×D = D×C = I, onde I é matriz identidade. Depois resolvemos os dois sistemas de equações resultantes.

Observe que a matriz C codificou a mensagem multiplicando a matriz M pela direita, então, temos que decifrar a mensagem multiplicando por D=C^-1 também pela direita, pois a propriedade comutativa no produto de matrizes não é válida. Decodificando a mensagem 51 81 9 14, encontramos:

Logo, a mensagem 51 81 9 14 será compreendida como 21 9 4 1 , correspondendo a palavra VIDA.
A alternativa (D) é a opção correta.

---

Exercícios Matrizes

matrizes (operações) exercícios

Nesse artigo será abordado operações com matrizes, tipos de matrizes e alguns exercicios de vestibulares passados para fixação da matéria e preparação para o vestibular.

Matrizes 

As matrizes são estruturas matemáticas organizadas na forma de tabela com linhas e colunas, utilizadas na organização de dados e informações e dispostos em m linhas e n colunas. 

, matriz de ordem 3 x 1. (3 linhas e 1 coluna).

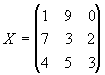, matriz de ordem 3 x 3. (3 linhas e 3 colunas).

, matriz de ordem 4 x 2. (4 linhas e 2 colunas)

Transposta de uma matriz A : é a matriz A^t obtida de A permutando-se as linhas pelas colunas e vice-versa.

Exemplo:

A matriz A^t é a matriz transposta da matriz A .

Adição de matrizes 

Esta operação só pode ser feita com matrizes de mesmo número de linhas e mesmo número de colunas (mesma ordem). A soma dessas matrizes irá resultar em outra matriz que também terá o mesmo número de linhas e de colunas. 

Os termos deverão ser somados com os seus termos correspondentes.
Concluímos que:
Dada duas matrizes, A e B, as duas de ordem m x n. Então, A + B = C, com
C de ordem m x n ↔ a11 + b11 = c11.

Observe os exemplos seguintes para melhor compreensão.

Exemplo: Dadas as matrizes abaixo, efetue A + B.

Solução: Temos que:

Subtração de matrizes

Dadas duas matrizes de mesmo tipo, A e B, denomina-se matriz diferença (A-B) a matriz obtida subtraindo-se os elementos correspondentes de A e B. As matrizes subtraídas devem ter a mesma ordem (mesmo número de linhas e colunas) e a matriz obtida com a subtração (matriz diferença) também deve ter o mesmo número de linhas e colunas que as matrizes subtraídas.

Concluímos que:

Dada duas matrizes, A e B, as duas de ordem m x n. Então A – B = C de
ordem m x n ↔ a11 – a11 = c11

Exemplo: Considerando as matrizes abaixo, efetue A – B.

Solução: Temos que:

 

Produto das matrizes

Dada uma matriz A = (aij)mxn e um número real k, denomina-se matriz produto do numero real K por A, a matriz obtida multiplicando-se cada um dos seus elementos por k.

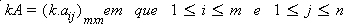
Em outras palavras, cada elemento de C é calculado multiplicando-se ordenadamente os elementos da linha i da matriz A pelos elementos correspondentes da coluna j da matriz B e , a seguir, somando-se os produtos obtidos. Veja abaixo:

Vamos mostrar o produto de matrizes com um exemplo:

Onde L1C1 é o produto escalar dos elementos da linha 1 da 1ª matriz pelos elementos da coluna1 da segunda matriz, obtido da seguinte forma:

L1C1 = 3.2 + 1.7 = 13. Analogamente, teríamos para os outros elementos:
L1C2 = 3.0 + 1.5 = 5
L1C3 = 3.3 + 1.8 = 17
L2C1 = 2.2 + 0.7 = 4
L2C2 = 2.0 + 0.5 = 0
L2C3 = 2.3 + 0.8 = 6
L3C1 = 4.2 + 6.7 = 50
L3C2 = 4.0 + 6.5 = 30
L3C3 = 4.3 + 6.8 = 60, e, portanto, a matriz produto será igual a:

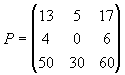
O produto entre duas matrizes A e B é definido se , e somente se, o número de colunas da matriz A for igual ao numero de linhas da matriz B. Assim:

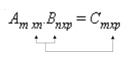
MATRIZ QUADRADA

 É A MATRIZ CUJO NÚMERO DE LINHAS É IGUAL AO DE COLUNAS. PORTANTO, SE AM×N É QUADRADA, M = N. EXEMPLO:

QUANDO A MATRIZ É QUADRADA NELA PODEMOS PERCEBER A PRESENÇA DE UMA DIAGONAL SECUNDÁRIA E UMA DIAGONAL PRINCIPAL. 

MATRIZ IDENTIDADE

Para que seja uma matriz identidade uma matriz tem que ser quadrada do tipo: 2x2 , 3x3, 4x4, etc. e os elementos da diagonal principal devem ser iguais a 1 e os outros elementos iguais a 0.

Exemplo:

                          

Matriz diagonal

Para que seja uma matriz diagonal uma matriz tem que ser quadrada do tipo: 2x2, 3x3, 4x4, etc. e os elementos que não são da digonal principal devem ser iguais a zero.

Matriz inversa

Considere uma matriz quadrada A de ordem n. Se existir uma matriz quadrada B, da mesma ordem, tal que:   AB = In    sendo In a matriz identidade, ou seja, uma matriz terá uma matriz inversa se for quadrada e se o produto das duas matrizes for igual a uma matriz identidade quadrada de mesma ordem das outras.

Então a matriz B será chamada inversa da matriz A, sendo indicada por A^{(-1). Nesse caso dizemos que a matriz é inversível. Se não existir a matriz B, dizemos que a matriz A não tem inversa, ou seja, não é inversível. Se a matriz inversa existir, ela é única.}

^Exemplo:

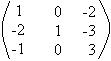^{Determinar, se existir, a inversa da matriz A =}  e B= são inversas entre si.

Para que seja verdade o produto de G . K = I₃



Portanto, concluímos que as matrizes A e B são inversas entre si.

      

Exercícios Matrizes

1) Multiplicando-se uma matriz 3 x 4 por uma matriz 4 x 5 obtém-se uma matriz de que tipo?
                                                                                                                                      a  a
2) (UNICAMP) Supondo a ≠ 0, determine x tal que A² = 0, onde A é a matriz A = (x x ).

3) Na matriz B = (bij)3x3, onde bij = -2, se i < j , calcule a12*a22*a32.
                                                     5i, se i = j
                                                     3ij, se i > j

4) Adicione as matrizes e determine os valores das incógnitas.

5) (MACK) Se A é uma matriz 3 x 4 e B uma matriz n x m, então:
 
a) existe A + B se, e somente se, n = 4 e m = 3;
b) existe AB se, e somente se, n = 4 e m = 3;
c) existem AB e BA se, e somente se, n = 4 e m = 3;
d) existem, iguais, A + B e B + A se, e somente se, A = B;
e) existem, iguais, AB e BA se, e somente se, A = B.

6) (PUC) Se A, B e C são matrizes quadradas e At, Bt e Ct são suas matrizes transpostas, e igualdade falsa entre essas matrizes é:

a) (A = B) . C = A . C + B . C
b) (A + B)^t = A^t + B^t

c) (A . B)^t = A^t . B^t

d) (A - B)C = AC - BC

e) (A^t)^t = A

7) Caso exista, encontre a inversa da matriz 

Gabarito: 
1) 3 x 5   2) x = - a ou x = 0  3) - 360  4) x = 5  y = - 4   t = 1  z = 6   5) C  6) C  7)

Quem Faz aniversario e quem vai fazer

AMANHÃ, 13 DE SETEMBRO

Isabelle Stanzione

fazendo 18 anos de idade

Inna Rodrigues

fazendo 37 anos de idade

SEGUNDA, 15 DE SETEMBRO

Jessica Pontes

fazendo 17 anos de idade

TERÇA, 16 DE SETEMBRO

Marcos Giggios

Davi Vinicius

fazendo 15 anos de idade

QUARTA, 17 DE SETEMBRO

Ana Letícia

fazendo 17 anos de idade

Lucia Santos

fazendo 47 anos de idade

QUINTA, 18 DE SETEMBRO

Vera Oliveira

fazendo 55 anos de idade

Isabelly Nery

fazendo 16 anos de idade